Sum Tree

Sum tree is a data structure based on binary heap. Besides basic heap properties, the value of each node in a sum tree equals to the sum of the values from the two child nodes. DeepMind used this data structure to efficiently sample data according to their priorities^[1]. Concretely, nodes with higher value (priority) are more likely to be sampled in a sum tree. The time complexity of sampling and updating a sum tree is $O \left( \log n \right)$, where $n$ is the number of nodes in the tree. Here is one example implementation of the data structure.

Definitions

Symbol	Description
$n$	Number of nodes in a sum tree.
$a_i \left( 1 \leqslant i \leqslant n \right)$	One specific node in a sum tree, where $i$ is the same as the index of the array representation of a binary heap, with $a_1$ indicating the root node, $a_{i2}$ indicating the left child of node $a_i$, and $a_{i2+1}$ indicating the right child of node $a_i$.
$parent \left( a_i \right)$	Parent node of node $a_i$.
$v \left( a_i \right)$	Value of node $a_i$. If $a_i$ is a leaf node, $v \left( a_i \right)$ is the priority of the data associated with it. Otherwise, $v \left( a_i \right)$ is the sum of the values from its two child nodes.
$P \left( a_i \right)$	Probability that node $a_i$ is visited (explained in the example below).

Example

Suppose we have a data set of 8 elements with priority values being 3, 10, 12, 4, 1, 2, 8, 2, respectively. Now we want to sample elements from this data set, and expect that elements with higher priority are more likely to be sampled. To solve this problem, we can build a sum tree below:

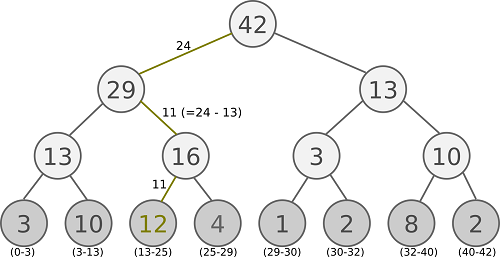
From the picture above, we can see that the tree has 8 leaf nodes storing the priority values of the 8 elements. The value of each inner node is the sum of the values from both child nodes. Therefore, the value of the root node is the sum of all priority values, which is 42.

To sample one element, we first uniformly sample a number within the interval [0, 42], and suppose we get the number 24. We then start at the root node and look at its left child (with value 29). Finding that 24 $\leqslant$ 29, we move from the root node to the left child. Looking at its left child (with value 13), we find 24 $\nleqslant$ 13, so we move to the right child (with value 16). Since we pass the left child, we subtract 13 from 24 and consider 11 (=24-13) as the new number for traversing. Sitting on the node with value 16, we look at the left child (with value 12) and find that 11 $\leqslant$ 12, so we move to the left child. Since we reach a leaf node, we sample the element with priority specified in the node. In this example, the element with priority 12 is sampled. Throughout the process, we have visited node $a_1$, $a_2$, $a_5$, and $a_{10}$.

The sampling process described above ensures that when $1 \leqslant i \leqslant n$,

$$ P \left( a_i \right) = \dfrac{v \left( a_i \right)}{v \left( a_1 \right)} \label{1} \tag{1} $$

Proof

Obviously, equation $\ref{1}$ holds when $i=1$ because the root node will always be visited:

$$ P \left( a_1 \right) = 1 = \dfrac{v \left( a_1 \right)}{v \left( a_1 \right)} $$

To prove equation $\ref{1}$ holds when $i>1$, we can start with a small sum tree with 3 nodes:

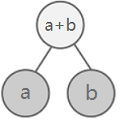
According to the sampling method, we start by sampling a number within the interval $ \left[ 0, a+b \right] $. Suppose we get the number $x$. If $x \leqslant a$, the left child will be sampled. Otherwise, we will sample the right child. Therefore,

$$ \begin{align} P \left( a_2 \right) &= P \left( 0 \leqslant x \leqslant a \right) = \dfrac{a}{a+b} = \dfrac{v \left( a_2 \right)}{v \left( a_1 \right)} \\ P \left( a_3 \right) &= P \left( a < x \leqslant a+b \right) = \dfrac{b}{a+b} = \dfrac{v \left( a_3 \right)}{v \left( a_1 \right)} \end{align} $$

Since every sum tree can be constructed recursively from several small sum trees mentioned above, we can derive that

$$ \begin{align} P \left( a_i \right) &= P \left( parent \left( a_i \right) \right) P \left( a_i \mid parent \left( a_i \right) \right) \\ &= P \left( parent \left( a_i \right) \right) \dfrac{v \left( a_i \right)}{v \left( parent \left( a_i \right) \right)} \quad \left( 1 \leqslant i \leqslant n \right) \end{align} \label{2} \tag{2} $$

We can solve equation $\ref{2}$ recursively:

$$ \begin{align} P \left( a_i \right) &= P \left( parent \left( a_i \right) \right) \dfrac{v \left( a_i \right)}{v \left( parent \left( a_i \right) \right)} \label{3} \tag{3} \\ P \left( parent \left( a_i \right) \right) &= P \left( parent \left( parent \left( a_i \right) \right) \right) \dfrac{v \left( parent \left( a_i \right) \right)}{v \left( parent \left( parent \left( a_i \right) \right) \right)} \label{4} \tag{4} \\ \dots \tag{...} \\ P \left( parent \left( \dots \right) \right) &= P \left( a_1 \right) \dfrac{v \left( parent \left( \dots \right) \right)}{v \left( a_1 \right)} \label{k} \tag{k} \end{align} $$

Multiply equations $\ref{3} \thicksim \ref{k}$. We can get:

$$ P \left( a_i \right) = P \left( a_1 \right) \dfrac{v \left( a_i \right)}{v \left( a_1 \right)} = \dfrac{v \left( a_i \right)}{v \left( a_1 \right)} $$

Therefore, equation $\ref{1}$ holds when $i>1$ as well.

In conclusion, equation $\ref{1}$ holds when $1 \leqslant i \leqslant n$.

Symbol	Description
\(n\)	Number of nodes in a sum tree.
\(a_i \left( 1 \leqslant i \leqslant n \right)\)	One specific node in a sum tree, where \(i\) is the same as the index of the array representation of a binary heap, with \(a_1\) indicating the root node, \(a_{i2}\) indicating the left child of node \(a_i\), and \(a_{i2+1}\) indicating the right child of node \(a_i\).
\(parent \left( a_i \right)\)	Parent node of node \(a_i\).
\(v \left( a_i \right)\)	Value of node \(a_i\). If \(a_i\) is a leaf node, \(v \left( a_i \right)\) is the priority of the data associated with it. Otherwise, \(v \left( a_i \right)\) is the sum of the values from its two child nodes.
\(P \left( a_i \right)\)	Probability that node \(a_i\) is visited (explained in the example below).